Lugar Geometrico

DISEÑO DE CONTROL MEDIANTE EL MÉTODO DEL LUGAR GEOMÉTRICO DE LAS RAÍCES.

El objetivo de esta práctica es utilizar el entorno RLTOOL de matlab 5.3 para realizar el diseño de sistemas de control de una manera sencilla y rápida. Para ello se utiliza la técnica del lugar geométrico de las raíces.

Desarrollo:
Sea el sistema:
2
G(s) = ---------------------
s^2 + 3 s + 2
Se desea modelar un controlador de tal manera que el sistema controlado tenga una respuesta transitoria en el tiempo a una entrada escalón unitario con un máximo sobreimpulso Mp de un 5%, y con un tiempo Ts de asentamiento al 2% de 2 segundos.

Visualización del sistema en RLTOOL.

» s=tf('s')

Transfer function:
s

» Gs=2/(s+1)/(s+2)

Transfer function:
2
-------------------
s^2 + 3 s + 2
» rltool

En FILE /IMPORT MODEL.
Seleccionar y cargar Gs en el bloque P.

a) Visualizar las restricciones en el plano S.
Mp = 0.05
Factor de amortiguamiento = 0.69
Ts(2%)=2 s
Frecuencia natural = 2.9 r/s

Gc=Kp

b) Si adicionamos un polo.

Kp
Gc = -------------------
(S+p)

c) Si adicionamos un cero.

Gc=Kp(s+z)

d) Adición de un polo y un cero (en atraso)
Kp(s+z)
Gc = -------------------
(s+p)
Donde z es mayor que p

e) Adición de un polo y un cero (en adelanto).
Kp(s+z)
Gc = -------------------
(s+p)

Donde z es menor que p

f) Compensador de adelanto
Para obtener los parámetros del compensador en adelanto ubicamos el polo y el cero de tal manera que el lugar geométrico de las raíces se intercepte con las restricciones en el plano s. Luego ubicamos los polos de lazo cerrado sobre la intersección.

Finalmente tomamos los datos del compensador de adelanto que aparece en la ventana del RLTOOL.
2.9822 (s+2.41)
Gc =---------------------------
(s+3.58)

g) evaluando la respuesta al escalón.
Preguntas:

1.-Se puede efectuar el control del sistema mostrado en clase por medio de un compensador en atraso? Argumente.
No se puede por que para ello necesitaremos del compensador de atraso que tiene la siguiente forma y condición:

Donde z es mayor que p

Y guiándonos de esa forma y condición se busco efectuar el control del sistema por medio de un compensador en atraso y se observo que cada vez que tratábamos de establecer esta condición de z mayor a p, el lugar geométrico de las raíces se aleja de la intersección entre la frecuencia natural y el factor de amortiguamiento, sin lograrlo interceptar, esto al tratar de mover z y p.

2. Existe un rango definido sobre los cuales se pueden mover el polo y el cero de un compensador o las respuestas son múltiples?
No existe un rango definido por ello diremos que existen respuestas múltiples; respuestas múltiples pues el diseño no es único.

3. De que orden es el sistema controlado?
El sistema controlado es el resultado de planta y el controlador. El sistema controlado o compensado es de tercer orden.

4. Si el orden cambia, por que se siguen analizando los polos del sistema de compensador?
A pesar del cambio de orden se sigue analizando los polos del sistema sin compensar debido a que estos son la base del sistema para lo cual querremos un valor de factor de amortiguamiento y frecuencia natural.

5. Diseñar un compensador Gc para que se cumpla que el sistema Gs1 cumpla con tener un Mp del 20% y un Ts al 2% de 5 segundos.
(s+4)
Gs1 = -------------------
s(s2+3s+2)

» s=tf('s')

Transfer function:
s

» Gs1=(s+4)/s/(s^2+3*s+2)
Transfer function:
s + 4
-----------------
s^3 + 3 s^2 + 2 s

Hallando el factor de amortiguamiento y la frecuencia natural.
» z=-(log(0.2)/sqrt(pi^2+log(0.2)^2))
z =

0.4559
» wn=4/(5*z)

wn =

1.7546

2.5137 (s+1.03)
Gc =---------------------------
(s+2.91)

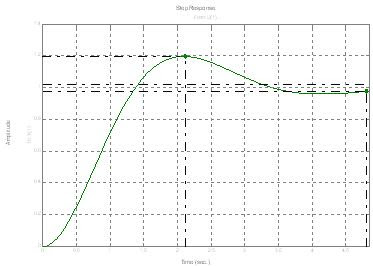Mp=0.2 y Ts=4.8s