En numerosas ocasiones es necesario convertir la energía eléctrica en energía mecánica, esto se puede lograr, por ejemplo, usando los motores de corriente continua. Pero cuando lo deseado es posicionamiento con un elevado grado de exactitud y/o una muy buena regulación de la velocidad, se puede contar con una gran solución: utilizar un motor paso a paso.
El desarrollo de la presente investigación tiene por objeto dar a conocer los principios básicos de funcionamiento de este tipo de motores, sus características constructivas y las formas básicas de hacer funcionar los motores por medio de dispositivos microcontroladores.
Sus principales aplicaciones se pueden encontrar en robótica, tecnología aeroespacial, control de discos duros, flexibles, unidades de CD-ROM o de DVD e impresoras, en sistemas informáticos, manipulación y posicionamiento de herramientas y piezas en general.
Los motores paso a paso son ideales para la construcción de mecanismos en donde se requieren movimientos muy precisos.
La característica principal de estos motores es el hecho de poder moverlos un paso a la vez por cada pulso que se le aplique. Este paso puede variar desde 90° hasta pequeños movimientos de tan solo 1.8°, es decir, que se necesitarán 4 pasos en el primer caso (90°) y 200 para el segundo caso (1.8°), para completar un giro completo de 360°.
Estos motores poseen la habilidad de poder quedar enclavados en una posición o bien totalmente libres. Si una o más de sus bobinas están energizadas, el motor estará enclavado en la posición correspondiente y por el contrario quedará completamente libre si no circula corriente por ninguna de sus bobinas.
El motor paso a paso está constituido esencialmente por dos partes: a) Una fija llamada "estator", construida a base de cavidades en las que van depositadas las bobinas que excitadas convenientemente formarán los polos norte-sur de forma que se cree un campo magnético giratorio. b) Una móvil, llamada "rotor" construida mediante un imán permanente, con el mismo número de pares de polos, que el contenido en una sección de la bobina del estator; este conjunto va montado sobre un eje soportado por dos cojinetes que le permiten girar libremente.
Si por el medio que sea, conseguimos excitar el estator creando los polos N-S, y hacemos variar dicha excitación de modo que el campo magnético formado efectúe un movimiento giratorio, la respuesta del rotor será seguir el movimiento de dicho campo, produciéndose de este modo el giro del motor.
Puede decirse por tanto que un motor paso a paso es un elemento que transforma impulsos eléctricos en movimientos de giro controlados, ya que podremos hacer girar al motor en el sentido que deseemos y el número de vueltas y grados que necesitemos.
PRINCIPIO DE FUNCIONAMIENTO
Los motores eléctricos, en general, basan su funcionamiento en las fuerzas ejercidas por un campo electromagnético y creadas al hacer circular una corriente eléctrica a través de una o varias bobinas. Si dicha bobina, generalmente circular y denominada estator, se mantiene en una posición mecánica fija y en su interior, bajo la influencia del campo electromagnético, se coloca otra bobina, llamada rotor, recorrida por una corriente y capaz de girar sobre su eje, esta última tenderá a buscas la posición de equilibrio magnético, es decir, orientará sus polos NORTE-SUR hacia los polos SUR-NORTE del estator, respectivamente. Cuando el rotor alcanza esta posición de equilibrio, el estator cambia la orientación de sus polos, aquel tratará de buscar la nueva posición de equilibrio; manteniendo dicha situación de manera continuada, se conseguirá un movimiento giratorio y continuo del rotor y a la vez la transformación de una energía eléctrica en otra mecánica en forma de movimiento circular.
Aún basado en el mismo fenómeno, el principio de funcionamiento de los motores de corriente continua, los motores paso a paso son más sencillos si cabe, que cualquier otro tipo de motor eléctrico.
La figura 1 intenta ilustrar el modo de funcionamiento de un motor paso a paso, suponemos que las bobinas L1 como L2 poseen un núcleo de hierro dulce capaz de imantarse cuando dichas bobinas sean recorridas por una corriente eléctrica. Por otra parte el imán M puede girar libremente sobre el eje de sujeción central.
 Figura 1. Principio de funcionamiento de un motor paso a paso
Figura 1. Principio de funcionamiento de un motor paso a paso Inicialmente, sin aplicar ninguna corriente a las bobinas (que también reciben el nombre de fases) y con M en una posición cualquiera, el imán permanecerá en reposo si no se somete a una fuerza externa.
Si se hace circula corriente por ambas fases como se muestra en la Figura 1(a), se crearán dos polos magnéticos NORTE en la parte interna, bajo cuya influencia M se desplazará hasta la posición indicada en dicha figura.
Si invertimos la polaridad de la corriente que circula por L1 se obtendrá la situación magnética indicada en la Figura 1(b) y M se verá desplazado hasta la nueva posición de equilibrio, es decir, ha girado 90 grados en sentido contrario a las agujas del reloj.
Invirtiendo ahora la polaridad de la corriente en L2, se llega a la situación de la Figura 1 (c) habiendo girado M otros 90 grados. Si, por fin, invertimos de nuevo el sentido de la corriente en L1, M girará otros 90 grados y se habrá obtenido una revolución completa de dicho imán en cuatro pasos de 90 grados.
Por tanto, si se mantiene la secuencia de excitación expuesta para L1 y L2 y dichas corrientes son aplicadas en forma de pulsos, el rotor avanzará pasos de 90 grados por cada pulso aplicado.
Por lo tanto se puede decir que un motor paso a paso es un dispositivo electromecánico que convierte impulsos eléctricos en un movimiento rotacional constante y finito dependiendo de las características propias del motor.
El modelo de motor paso a paso que hemos analizado, recibe el nombre de bipolar ya que, para obtener la secuencia completa, se requiere disponer de corrientes de dos polaridades, presentando tal circunstancia un inconveniente importante a la hora de diseñar el circuito que controle el motor. Una forma de paliar este inconveniente es la representada en la Figura 2, obteniéndose un motor unipolar de cuatro fases, puesto que la corriente circula por las bobinas en un único sentido.
Si inicialmente se aplica la corriente a L1 y L2 cerrando los interruptores S1 y S2, se generarán dos polos NORTE que atraerán al polo SUR de M hasta encontrar la posición de equilibrio entre ambos como puede verse en la Figura 2(a). Si se abre posteriormente S1 y se cierra S3, por la nueva distribución de polos magnéticos, M evoluciona hasta la situación representada en la Figura 2(b).
 Figura 2.- Principio básico de un motor unipolar de cuatro fases
Figura 2.- Principio básico de un motor unipolar de cuatro fases Siguiendo la secuencia representada en la Figuras 2 (c) y (d), de la misma forma se obtienen avances del rotor de 90 grados habiendo conseguido, como en el motor bipolar de dos fases, hacer que el rotor avance pasos de 90 grados por la acción de impulsos eléctricos de excitación de cada una de las bobinas. En uno y otro caso, el movimiento obtenido ha sido en sentido contrario al de las agujas del reloj; ahora bien, si las secuencias de excitación se generan en orden inverso, el rotor girará en sentido contrario, por lo que fácilmente podemos deducir que el sentido de giro en los motores paso a paso es reversible en función de la secuencia de excitación y, por tanto, se puede hacer avanzar o retroceder al motor un número determinado de pasos según las necesidades.
El modelo de motor paso a paso estudiado, salvo su valor didáctico, no ofrece mayor atractivo desde el punto de vista práctico, precisamente por la amplitud de sus avances angulares.
Una forma de conseguir motores Paso a Paso de paso mas reducido, es la de aumentar el número de bobinas del estator, pero ello llevaría a un aumento del coste y del volumen y a pérdidas muy considerable en el rendimiento del motor, por lo que esta situación no es viable. Hasta ahora y para conseguir la solución más idónea, se recurre a la mecanización de los núcleos de las bobinas y el rotor en forma de hendiduras o dientes, creándose así micropolos magnéticos, tantos como dientes y estableciendo las situaciones de equilibrio magnéticos con avances angulares mucho menores, siendo posible conseguir motores de hasta de 500 pasos.

RESULTADOS:
*Fallidos
El primer inconveniente fue con el diagrama del circuito ya que los pines que debian alimentar no concordaban con los mencionados en otros controladores de motor paso a paso asi mismo usan los mismos Ckts. integrados. (Luego nos fuimos dando cuenta a medida que simulamos el circuito en PROTEUS)
Esto podemos entender como La inexperiencia que tenemos en trabajar con motores paso a paso nos llevo a utilizar un motor inadecuado(el diagrama fue para un bipolar y usamos unipolares) para observar mejor el rendimiento del controlador .
Usamos un controlador El L297 o el integrado que cumple la función de regulación corriente a suministrar al motor no se encontraba en óptimas condiciones ya que compramos "de segunda" por lo cual, el motor paso a paso ofrece menor paso y velocidad.
Cabe destacar que, el controlador funciono en un inicio en tiempo de pruebas, mas no en la presentacion del proyecto, lo cual hace dudar netamente de los componentes ya que la logica que usamos en un inicio estuvo bien aplicada y simulada respectivamente.
Recomendaciones:
* A los siguientes grupos de trabajos de esta índole, se les recomienda no usar componentes usados, pues no garantizan la continuidad de su trabajo, y fijarse bien al jugar con los nivles de tension.
Simulación en Proteus:
*He aquí el diagrama del circuito simulado exitosamente en PROTEUS:
Debido a que no se pudo adjuntar el archivo del circuito en PROTEUS, adjunto un video que muestra la simulación del mismo.




























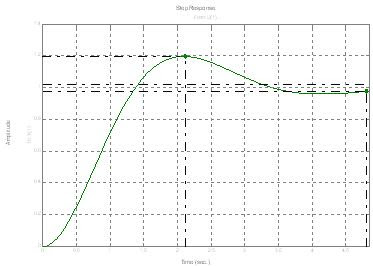
 La salida debería ser:
La salida debería ser: